Hiperbolas

Una hiperbola es el conjunto de Puntos en un plano cuya diferencia de sus ditancias a dos puntos fijos en el plano es costante. Los puntos fijos son los focos de la hiperbola. La linea que une los focos es el eje focal. El punto medio entre los focos es el centro. Los puntos donde la hiperbola se interseca con su eje focal son los vertices de hiperbola.

Hiperbola con centro (0,0)

Ecuacion estandar	(X^2/a^2) – (y^2/b^2)=1	(y^2/a^2) – (x^2/b^2)
Eje focal	Eje x	Eje y
Vertices	(±a,0)	(0,±a)
Focos	(±c,0)	(0,±c)
Semi eje transversal	a	a
Semi eje conjugado	b	b
Relacion pitagoricas	C^2= a^2 + b^2	C^2= a^2 + b^2
asintotas	Y= (±b/a) x	Y= (±b/a) x

Hiperbolas con centro (h,K)

Ecuacion estandar	(x-h)^2 / a^2 – (y-k)^2/ b^2=1	(y-k)^2/a^2 – (x-h)^2/ b^2
Eje focal	Y=k	X=h
vertices	(h±a,k)	(h, k±a)
focos	(h±c,k)	(h, k±c)
Semi eje transversal	a	A
Semi eje conjugado	b	B
Relacion pitagoricas	C^2= a^2 + b^2	C^2= a^2 + b^2
asintotas	Y= ±b/a (x-h)	Y= ±a/b (x-h)

Geometría Analítica : La Elipse

 

Ecuación de la elipse

Excentricidad

Ecuación reducida

De eje vertical

De eje horizontal y centro distinto al origen

De eje vertical y centro distinto al origen

Geometria analitica:

Se conoce como geometría analítica al estudio de ciertas líneas y figuras geométricas aplicando técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas.

La idea que llevó a la geometría analítica fue: a cada punto en un plano le corresponde un par ordenado de números y a cada par ordenado de números le corresponde un punto en un plano.

Fue inventada por René Descartes y por Pierre Fermat, a principios del siglo XVII, y como vimos, relaciona la matemática y el álgebra con la geometría por medio de las correspondencias anteriores.

Se utilizara estas dos formular: 

Ecuación estándar	(x-h)^2=4p(y-k)	(y-k)^2=4p(x-h)
Parábola abre:	Hacia arriba o abajo	Hacia izquierda o derecha
Foco:	(h+k,p)	(h + p,K)
Directriz:	Y=k-p	X=h-p
Eje:	X=h	Y=k
Diámetro focal:	4p	4p

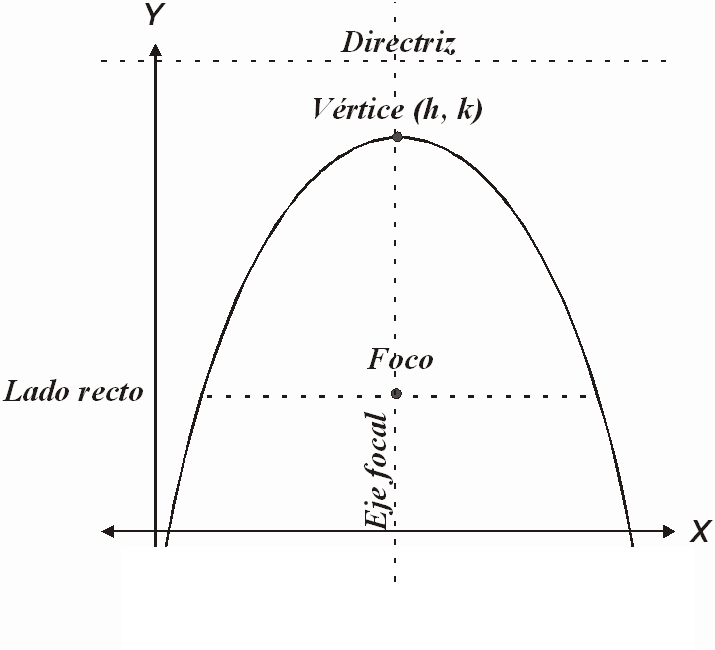
Ejemplo:
Determine el foco, vertice y la directriz de la parablola:
y^2+6x+2y+13
Y^2+2y+(2/2)^2=6x-13+(2/2)^2 (Vas a pasar a un lado las y con las Y y las X con las X)  (y se usara la funcion cuadratica en froma general: V=(b/2)^2
Y^2+2y+1=6x-13+1
(Y^2+2y+1)=6x-12
(Y+1)^2=6(x-2)
V=(2,-1)  -->cambian los signos porque no respeta signo.
Foco: (h+p,k)
(2+3/2, -1)
(7/2,-1)
Directriz: x= h-p (sustituir)
(2-3/2)
x+1
 Para sacar P:
Vas a dividir por 4p:
4p=6
4p/4=6/4 Se elimina el 4 y se simplifica
p=3/2
Ejemplo #2:
Determina la ecuacuin en forma estandar de la parabola que satistace las condiciones dados:
Foco:(-5,3) Vertice: (-5,6)
(x-h)^2=4p(y-k)
(x+5)^2=4p(y-6)
(x+5)^2=4(-3)(y-6)
(x+5)^2=-12(y-6)

Para sacar P=
k+p=3
6+p=3
p=3-6
p=-3

Geometria Analitica

Secciones Conicas

Una seccion conica es la interseccion de un plano y un cono. Dependiendo de la interseccion, se obtiene una conica determinada.

• Si la conica del plano es perpendicular al cono, se obtiene:

La Circunferencia

(Su ecuacion (la ecuacion del circulo) cuyo centro es en el origen es:  x²+y²=r²

• Si el plano se inclina ligeramente la figura que se obtiene es:

La Elipse

• Cuando el plano es paralelo a una recta sobre el cono, la curva resultante es:  

La Parabola

• Si el punto interseca dos ramas del cono, la curva resultante es: 

  
  

  

La Hiperbola

Ahora se hablara de cada una indivialmente:

LA PARABOLA 

La parabola es el conjunto de puntos del plano que esta a la misma distancia de un punto, su foco, y de una recta fija, su directriz. Los elementos son:

• El foco es el punto F
• La directriz es la recta d
• El eje de la parabola es la recta que pasa por el foco y es perpendicular a la directriz. Tambien es un eje de simetria.
• El vertice es el punto V en el que el eje corta a la parabola.

  
  

  

ECUACIONES DE LA PARABOLA CON VERTICE EN EL ORIGEN

 

FORMAS ESTANDAR PARA PARABOLA CON VERTICE (0,0)

Ejemplo:

Funciones Trigonometricas Inversas

Si f es una funcion uno a uno biunivoca con dominio A y rango B, entonces su inversa f ^- (f a la negativa) es la funcion con dominio B y rango A definida por:

f ^- (x)= y <=> f(y)= x

A) Funcion inversa del seno es la funcion sen ^-1  con diminio [-1,1 ] rango
[-π/2,π/2] definido por:
sen ^-1 = y <=> sen y = x

La funcion inversa del seno se llama arco seno (arcsen)

B) Funcion inversa del coseno es la funcion cos ^-1 con dominio [-1,1 ] y rango [0,  π]
definido por:
cos^-1 x = y <=> cos y = x

La funcion inversa del coseno se llamas arco coseno (arc cos)

C) Funcion inversa de la tangente es la funcion tan ^-1 con dominio en lR (reales) y rango [-π/2, π/2] definido por:
tan ^-1 x = y <=> tan y = x

La funcion inversa de tan se llama arco tangente (arctan).

Las funciones inversas de secante, cosecante y cotangente son las siguientes:

1) y= sec x, 0 ≤ x <  π/2, π ≤ x < 3π/2 => y = sec ^-1 x (arcsec)
2) y= csc x,0  ≤ x ≤  π/2, π<x≤3π/2 => y = csc ^-1 (arcccsc)
3)y= cot x, 0<x≤π, => y = cot ^-1 (arccot)